scala

Scala 'fun' error handling

An interesting article about error handling in a functional way in Scala and some ideas that make it possible to deal with failures in a very simple, opinionated and explicit way.

Antonio Murgia

Jul 13, 2020

Big data coding Development Knowledge Base scala TECH ARTICLE

This is the first post of a series about error handling in a functional way in Scala.

Dealing with failures is one of the harshest things we face in life. Coding is not different than living: at some point, things will go bad and as a software practitioner, you should expect such failures and be prepared. You will never remember when your application ran fine for years without crashing or producing bugs, but you will surely remember the problem that woke you up in the middle of the night and that could’ve been easily avoided by properly dealing with errors and failures in advance.

As a software engineer, I’ve seen my code failing many more times that I would like to admit, almost every piece of technology that your code interacts with, or is made of, can fail. The big difference between stable and fragile applications (when it comes to “code”) is in how they deal with failures.

In this post series (that was born from a workshop I kept at my company) I will show a couple of ideas that make it possible to deal with failures in a very simple, opinionated and explicit way. All of this without sacrificing code readability and composability. The code snippets are written in Scala, a JVM language made (in)famous by Apache Spark, which is our favourite data processing framework at AgileLab, and a functional programming library for Scala named Cats ?.

Disclaimer

Tech stack used in the snippets:

Scala 2.11
Typelevel Cats 2.0.0 (which is cross-published among 2.11, 2.12 and 2.13)

What this article is not:

A guide to Typelevel Cats
A category theory article

My objective is to be pragmatic, I want you to read this article and then try these things (and hopefully profit from them).

Our Legacy

Scala is a JVM language with full-interop with Java, therefore we cannot start an article about error handling in functional Scala without explaining how errors are dealt with in Java.

Checked Exceptions

If I try to write a simple program in Java that reads the first 3 lines of a txt file, I come across a very nice feature of the Java programming language: checked exceptions!

This code does not compile ?

Why is that? That’s because some methods that we are using explicitly declare to throw exceptions. In fact, if we give a look at the FileReader constructor signature:

If you’ve ever written any Java, you know that there is an “easy” solution to this problem:

Adding the throws clause to your method definition is enough to make someone else care about the exception.

We have a saying in Italy: Fatta la legge trovato l’inganno that in English translates into something like: Every law has a loophole.

In fact, not all Java exceptions have this useful property (that reflects in the method signature): there are also unchecked exceptions that do not “annoy” the programmer and therefore tend to be ubiquitous.

A very bad and very common practice, in fact, is the following:

Please never do that! You are hiding the fact that the print3lines method can fail, and this is a piece of information that is really precious for whoever is using that method.

Even if checked exceptions are somehow “good” because they appear in the method signatures, exceptions in general are a “bad idea” to deal with expected errors (i.e. parsing a String into a Int , which can fail in obvious and totally unexpected ways), since every thrown exception is an uncoditional jump to the first caller that handles it. And we don't like uncoditional jumps in our code, otherwise we would code in asm ?

To summarize what we have seen so far:

What about Scala?

Scala is based on the JVM and it’s interoperable with Java, but it has some fundamental differences, one of which is in how it handles exceptions. Scala has ONLY unchecked exceptions.

But Scala also has an exceptional type system (pun intended). Let’s leverage it!

In order to dive deeper in what I’m going to present you, we will need to learn a couple of concepts. Don’t be scared, that’s easy stuff!

ADT — Algebraic Data Types

Quoting from Wikipedia:

In computer programming, especially functional programming and type theory, an algebraic data type is a kind of composite type, i.e., a type formed by combining other types.

Two common classes of algebraic types are:

Product Types (tuples and records)
Sum Types (tagged/disjoint unions or coproducts)

I know, the names are scary, but in fact they embody a really simple concept. Let’s start from the idea that types are domains. For example, the Boolean type domain is {true, false}, while Int domain is [-2³¹, 2³¹). Unit domain, which is the Scala version of void, is only: (), Nothing (which is the type without instances) it's an empty domain. Each of these domains is finite and therefore has a size (all types are finite domains, since computer memory is finite).

Product types in Scala are case classes or tuples, and they do exactly what you expect them to do with the domain of their inner types:

Sum types in Scala are sealed hierarchies or enumerations, and they do exactly what you expect them to do with the domain of their inner types:

Now, it’s enough with the theory, why is this important?

We keep “domain”s of every function in your head while reasoning about code
The smaller the domains, the easier the reasoning and (also) built-in docs
If you want to stress this, have a look at refined

. . .

So, back to “checked exceptions”, in Scala we can emulate them at the type level as follows:

which is logically equivalent to its Java counterpart:

If you configure the Scala compiler to fail on warnings (i.e. -Xfatal-warnings) you will also get the same behaviour you would have when trying not to deal with checked exceptions in Java. In fact, if you try to write the following code:

Compilation fails due to:

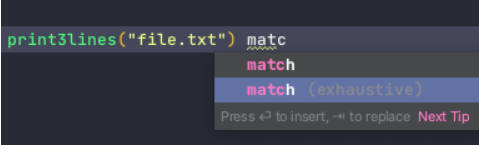
Since the error is now encoded in the type system, it’s very easy for IDEs to help you deal with it:

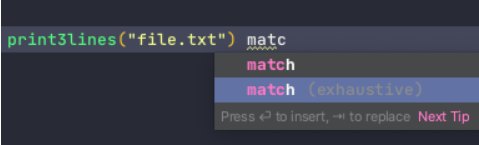
Ok, but that is a lot of boiler-plate!

That’s why Scala has built-in generic sum types that come to help:

Option[A]
Either[A, B]

`Option[A]`

Either[A, B]

Even if Option might not be the best option (my puns are always intended) to deal with failures, or things that "went wrong", they can be fine when we do not need in any way to communicate the "kind" of error that happened.

Using Either we can rewrite the previous toy program as follows:

Now let’s have a quick look at Either and Option and what they can offer us.

A (de)tour into `Either` and `Option`

If you are already “fluent” in Either and Option usage you can skip this chapter ?

Other than pattern matching, Either and Option offer many more idiomatic ways to interact with them.

Map

Option

Either

Right-biased map (default since Scala 2.12)

or Left-biased map

The effect of mapping a “side” (or projection) of the Either or an Option is:

if the “side” you’re trying to map is "empty" the computation is short-circuited

If the side is “populated” then the transformation is performed. Remember that if you map a Right, it is going to remain a Right and same applies for a Left: you can change the content, but not the type of the container.

flatMap

Option

Either

Right biased flatMap (default since Scala 2.12)

or Left biased flatMap

The effect of flatMapping a “side” (or projection) of the Either or an Option is:

if the “side” you are trying to flatMap is empty, the computation is short-circuited:

If the side is “populated” then the transformation is performed. Remember that using flatMap you are able to transform a Left into a Right or vice-versa.

`Either <-> Option`

Let’s reason about Option and Either in terms of ADTs ?

What is Option[A] domain?

A ⋃ {None}

What’s the domain of Either[L, R]?

R ⋃ L

They are quite similar, aren’t they? What if we pick a particular L ? For example let's pick Unit, the domain of Either[Unit, A] is:

A ⋃ {()}

Which carries the same quantity of information as Option[A].

If we all agree on this, we can say that it’s always possible to turn an Option into an Either providing the missing side value, and viceversa it's always possible to go from an Either to an Option "losing" one side of the Either. Thankfully Scala knows this better than us, therefore there are idiomatic ways of doing so:

If the option is empty you get Left(x), otherwise you get a Right with the content of the Option. Its dual operation is toLeft :

There are similar methods available on Either projections:

Getting out

When you get to the “end of the world” you will need to do something with the content of the Either and handle both cases (i.e. Left and Right).

We’ve already seen the most known way of “getting out” an Either which is match:

Another way to extract the result from an Either is to use fold:

or merge if A and B are of the same type (or you care about the first common supertype) which is the same as doing:

If instead of using match or folding, you are doing every time something like

you are defeating the purpose of using Either. If that happens, don't bother using Either ?.

The same applies to Option: calling Option.get defeats the purpose of using Option at all, because you are assuming that the Option is Some .

When someone tries to use Option.get in a pull request I'm watching pic.twitter.com/Thp9aVlaYC

— Jakub Kozłowski λ (@kubukoz) June 17, 2020

“Real life” programs

Ok, so far so good, but you haven’t shown me a real program — you might think — so let’s try to build something more complex.

Given a list of integers, if the sum of all elements is higher than 100, take the head and then multiply it by 30 otherwise multiply it by -30.

A very simple direct approach would be the following:

Let’s try to see this “program” from the caller perspective:

can it fail?
if it can fail, which are the error cases?

Looking only at the signature, the answer is: no, this program cannot fail. We have to look at the implementation to actually “spot” were errors can happen and exceptions can be thrown.

Another Approach

The error ADT

The implementation

or using some syntactic sugar:

Now, let’s try to answer the same questions:

can it fail?
if it can fail, which are the error cases?

Now we can answer the questions just looking at the signature!

Yes, the program can fail ( Either can be Right or Left) and there is just one failure case, the EmptyList.

Bonus — The best code is the code you don’t write

I’m not alone in thinking that the best code is the one you do not have to write or maintain. I would extend saying that the easiest error to handle is the one someone else handles for you. Like in the program we’ve just written, there are cases in which you can avoid to care about errors at all, because you make them not even possible restricting the input of your program.

How can we make our program infallible? Well, we can accept only non empty lists. Cats has what you need: NonEmptyList a list that cannot be empty (a.k.a. Nel ).

Now our program “cannot” fail because we pushed the accountability to obtain a non empty list to the boundaries of our program, we avoid at compile time the possibility to fail.

Very complicated programs

Let’s see now how we can compose a lot of functions that “return” Either, because if you are going to follow my hints, you're are going to compose a lot of Either s!

Let’s assume you have the following functions already implemented:

And you have to implement f combining all of them:

The most straightforward way to write the program would be something like the following:

A part for the fact that we are not dealing with errors and that this program does not compile at all, it surely has one big advance: the happy path is very “easy” to understand (this is why people say that exceptions are easy, they just ignore them most of the time), whoever reads this code can understand what’s going on. As Martin Fowler says:

Any fool can write code that a computer can understand. Good programmers write code that humans can understand.

We can use match to compose all our function calls like this:

But that’s a lot of boiler plate to write! It’s obvious that the first (wrong) implementation is much more readable.

We can try using flatMap then:

This indeed looks better, but to me it looks a lot like:

Let’s try with a for comprehension:

Do we agree that this implementation has the readability of the first (wrong) implementation and the advantages of actually dealing with errors in a way that reflects on the type system and therefore in the function signatures?

...

Conclusions — so far

Sticking to these practices is very easy to follow the business logic flow, without compromising on error handling. It is also straightforward to handle errors or just demand the caller to do so. Furthermore, totally avoiding exceptions allows us to not defensively try/catch every method call.

These patterns are particularly useful on Spark batch and streaming workloads were if only one out of 10 billion rows throws an exception the whole application will fail and/or retry to process the same data indefinitely wasting time and resources in vain.

That was enough for this chapter of the series (even if there weren’t any ? around)!

In the next post, we will see how we can combine functions which can fail in a way that is not fail-fast (i.e. stop at the first error) and also how to deal with collections of results.

Stay tuned!

Posted by Antonio Murgia

If you found this article useful, take a look at our Knowledge Base and follow us on our Medium Publication, Agile Lab Engineering!