Scala 'fun' error handling
An interesting article about error handling in a functional way in Scala and some ideas that make it possible to deal with failures in a very simple,...
Scala fun error handling. Part 2 - How to deal with failures when coding in Scala


Last time we saw how we can encode our results into Either or Option and then combine these results in a very simple and effective way. Our code looked like imperative, sequential code, but we always handled the possibility of failure that most functions have.
In this article, we will see that life is not sequential (not always at least) and how we can take care of non-sequential situations in a functional way.
Let’s recall the last exercise we solved:
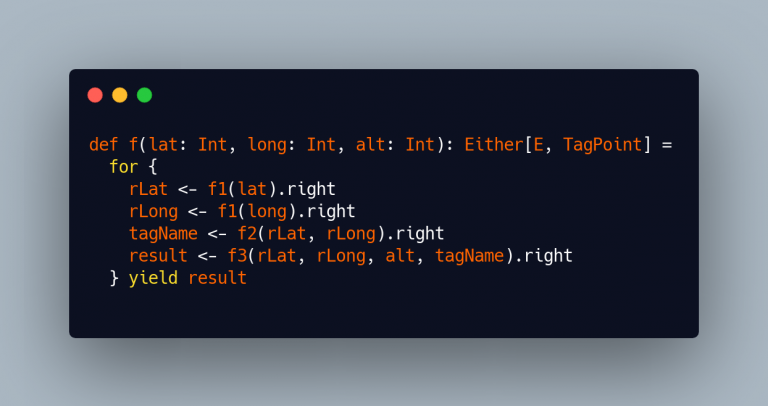
As it is (kind of) obvious, there aren’t any dependencies between the computation of rlatand rLong. Even if they are not dependant, in our last “solution” we don’t even bother checking the outcome of f1(long)if f1(lat) produces a Left, “thanks” to the short-circuiting property of Either.
In most cases, that would be a nice feature, but it’s not always the case. Sometimes you want to compute all the not inter-dependant paths and return all the errors (for example when you are validating an input form).
We can do it “by-hand” and provide a solution like the following:
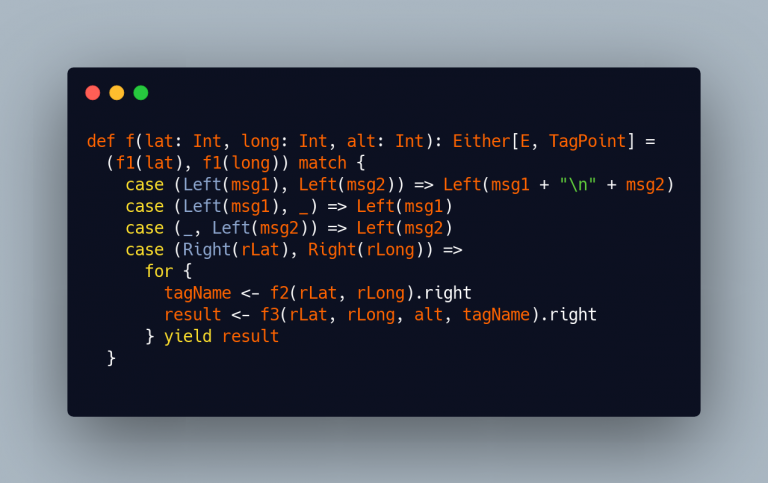
So, this works, but… It’s very cumbersome and doesn’t scale at all (if you had 3 results to compute and combine in parallel, you will have to write 8 (2³) cases instead of 4 (2²). There must be something easier and with better scaling properties!

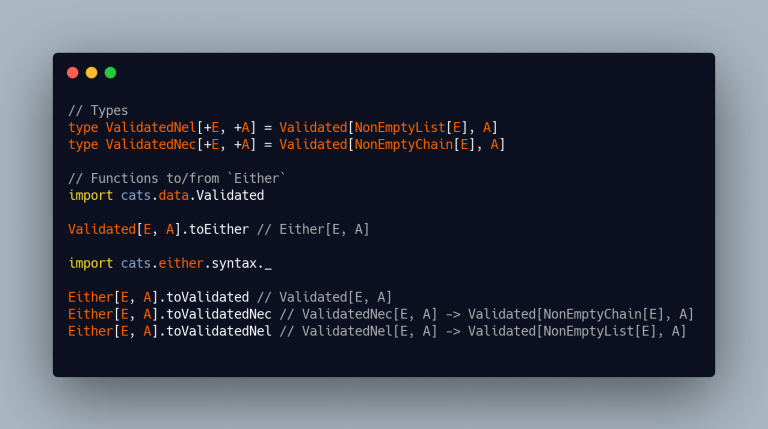
Validated is very similar to Either but with different “rules”. It also has very “nice” type aliases (we will see how useful they are later), and a couple of very handful methods and functions to create and convert them to/from Either:
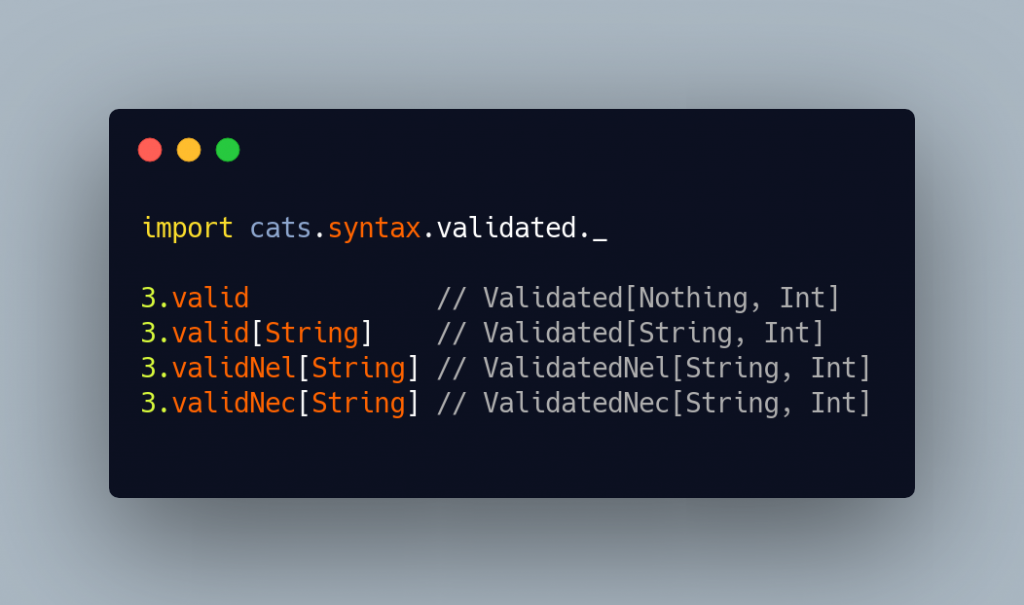
Ok, enough with the syntax, how do we use this Validated?
Let’s try to write the application of f1 to both lat and long parameters using Validated, we are going to do it step by step.
First of all, let’s define the signature
def applyF1ToBoth(lat: Int, long: Int): Either[E, (Double, Double)]
As we can see from the signature, we want to either fail with an E, or succeed with a pair of doubles.
Then, we apply the function to both latand long and place the results into a tuple, but not as Either, let’s transform them into ValidatedNonEmptyChain.
Why a ValidatedNonEmptyChain[E, Double]instead of a “simple” Validated[E, Double] (like the “original” return type, which is Either[E, Double])?
That is because we want to be able to combine a non-empty collection of errors (in our case it might be an error or no error at all, but the Chain data structure helps us to combine multiple errors).
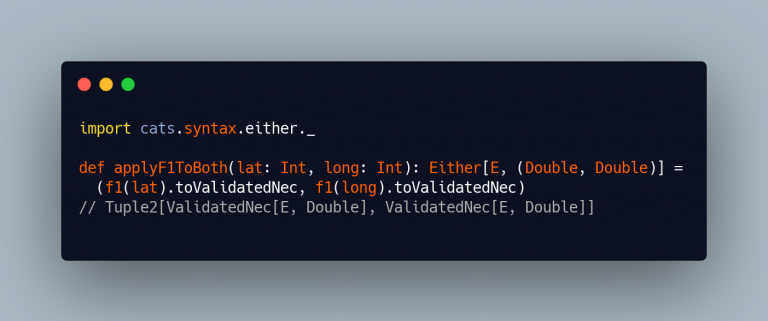
As we can see from the code snippet, we have now aTuple2[ValidatedNec[E, Double], ValidatedNec[E, Double]], quite different from the expected result, but don’t worry!
Now we need to take care of the results if they are both successful, and we do so using mapN:
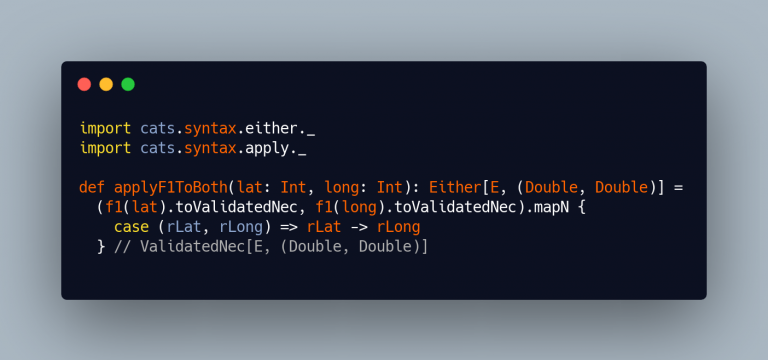
The solution now starts to take form. We can see it because the second generic argument of the ValidatedNec now resembles the one of the return type (Double, Double). Next step is to take care of the (possible) list of errors and reduce it to a single E (which in our case is String), to do so we are only going to concatenate the error strings, placing a n in between:
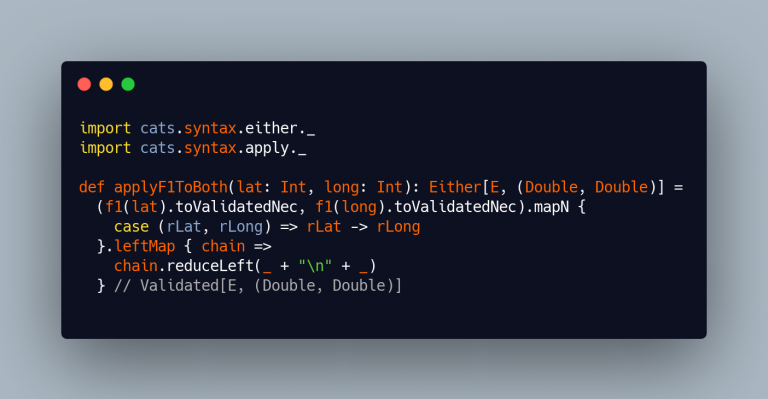
Ok, so far so good, we have a Validated instead of an Either, but this conversion is dead simple:
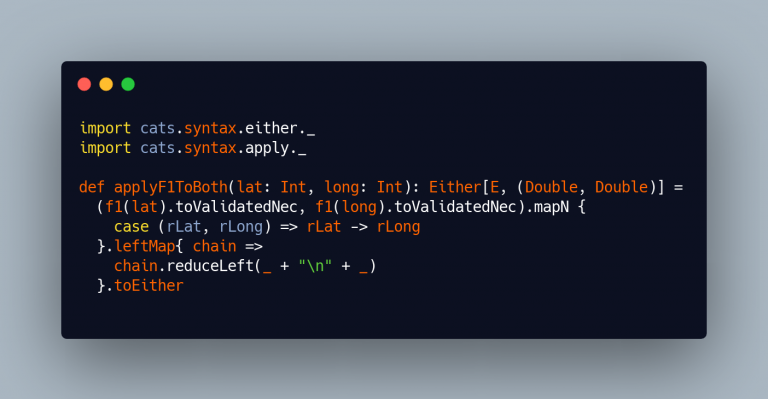
Done!
Now we can compose this new function with the “old” functions to obtain the final result:
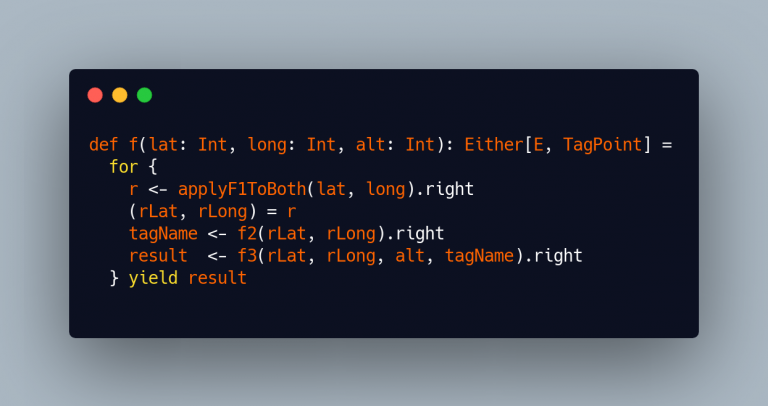
So we’ve just seen an approach that is:
- Less verbose than the match approach
- “Scales” up to 22 elements of any combined type
Validated[E,A] and Either[E, A] are “cousins”, they both express a computation that fails or succeeds in some way.
Disclaimer: in this paragraph I will swear a bit, because math is hard, but logical reasoning isn’t.
The main difference is on how they compose:
- with Either you stop at the first Left
- with Validated you go on aggregating Invalid
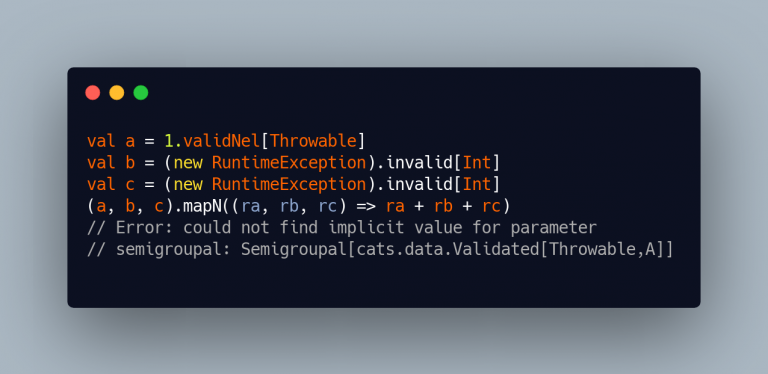
Unfortunately this aggregation ain’t free!
In fact, you cannot perform the mapNtrick in all cases:

From cats documentation:
Combine an `F[A]` and an `F[B]` into an `F[(A, B)]` that maintains the effects of both `fa` and `fb`
So, why Either always has a Semigroupal while Validateddoesn’t?
Either you stop at the first “error”, you don’t need any logic to aggregate errors because you just don’t aggregateValidated you have to “aggregate” the error part// Error: could not find implicit value for parameter
// semigroupal: Semigroupal[cats.data.Validated[Throwable,A]]
It is actually saying: “How do I do Throwable |+| Throwable”?
There is no “universal” meaning of
Throwable |+| Throwable
While it’s naturally there for:
NonEmptyChain[A] |+| NonEmptyChain[A]
This concept of “merge” or “combine” has a name, and it’s semigroup:
A “type” has a semigroup if it respects a rule (also known as law).
(a |+| b) |+| c == a |+| (b |+| c)

So whenever you define a custom semigroup, be sure to check that is really a semigroup (i.e. it’s associative). Just remember: aggregate things ⇨ Semigroup, in cats it is encoded as a typeclass: Semigroup[A]
cats already has semigroups for a lot of types:
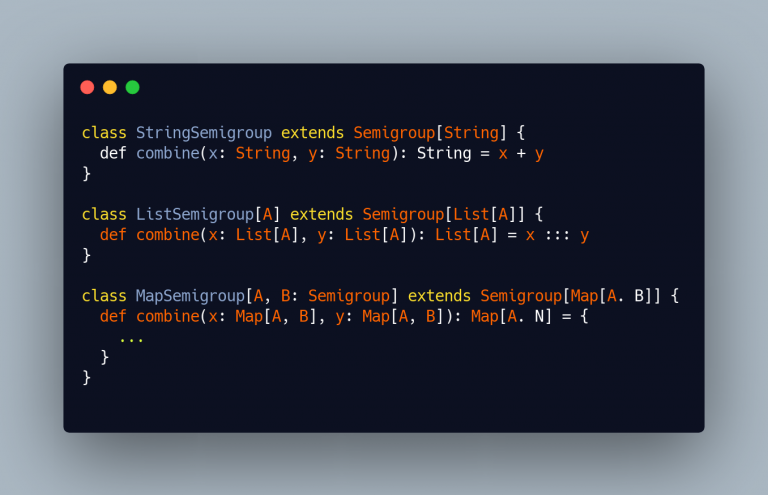
TIP: If you are tempted to code a Semigroup instance for a “primitive” type because cats doesn’t have one, think twice: it’s very likely that you are creating an unlawful (or was it chaotic?) Semigroup
For the most adventurous ones, the concepts that we just see correspond to the name of:
Yeah, I know the names are scary… I personally go with intuitions and then in the end figure out the theory.
You might already have figured out that namespaces follow this convention:
cats.syntax.${thing}._: contains all extension methods for that “thing” (not only data structures but also typeclasses like applyfor mapN )cats.instances.${thing}._: contains all “universal”: instances for that “thing” ( cats.instances.list._ contains Semigroup[List[A]])There is a running joke/non-joke in the FP community, which is:
It’s always traverse

So I think it is very useful to spend two words to explain what is traverse and how can be exploited.
Traverse has the ability to “turn inside out” things that are “traversable” which contain things that can be “mapped over”.
For example, did it ever occurred to you the need to do some of these things?
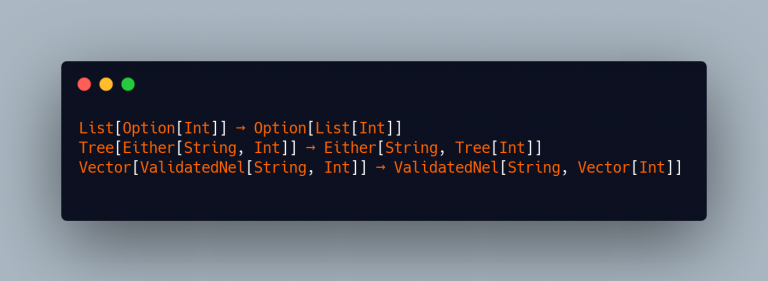
Start easy with Option :
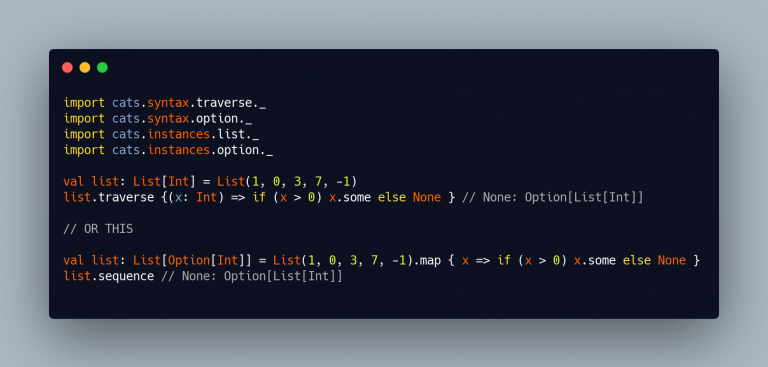
How does this work?
That’s possible because:
Traverse[List[_]]_Applicative[Option[_]]_So, is it possible to do the same with Either?
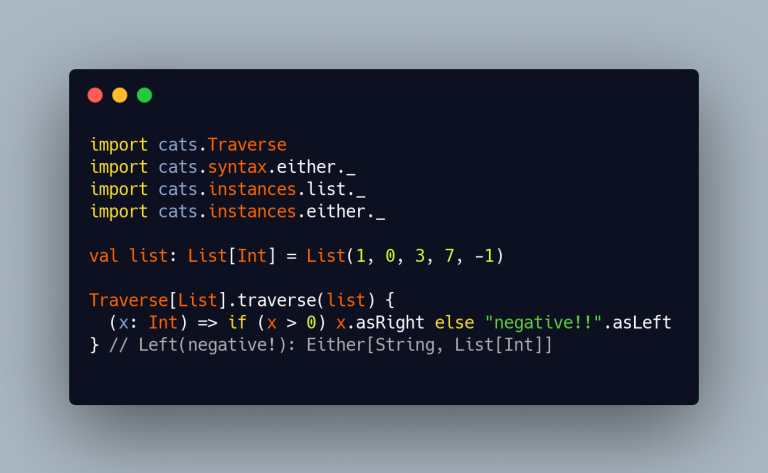
That’s possible because:
Traverse[List[_]] existsApplicative[Either[E, _]] existsEmust be fixed, there must be just one “hole”I guess we can do kind of the same with Validatedtoo…
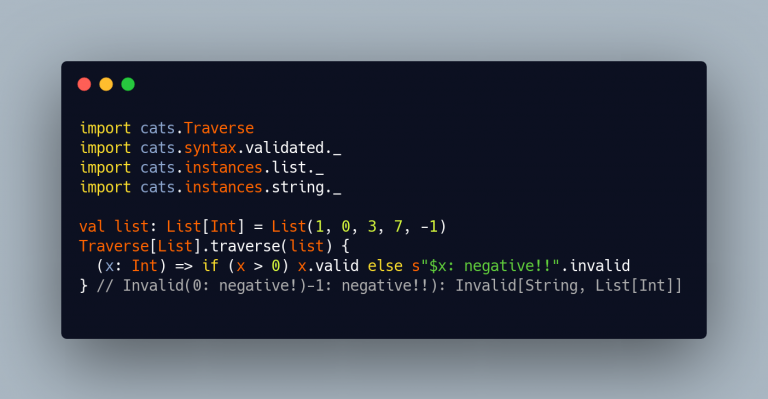
Sure!
That’s possible because:
Traverse[List[_]]_Applicative[Validated[E, _], A]ApplicativeError[Validated[E, _], A]andSemigroup[E]So:
ApplicativeError[F[_], E] + Semigroup[E] = Applicative[F[_], A]
And that is automatically solved by Scala implicits ❤️
But I usually obtain the same things “manually”
This means you need them, but you have your custom “rules” that only your team knows.
cats is “universally accepted”
So now every function will return an
Eitheror aValidatedandExceptions are never thrown?
No, my personal advice, is:
Either in signaturesValidated when you need to mapNI didn’t, we will see how to handle REAL exceptions in a principled and typesafe manner, but not today.
The thing is:
For that there might be other articles in the Future[_]
Finally, I’ll leave you with a couple of @impurepics pics, because if you got till here, you deserve it.
What our business logic should look like:

If you made it this far, you may be interested in Part 1 or in other tech articles that you can find on our Knowledge Base page.
Stay tuned because other articles are coming!
Posted by Antonio Murgia
An interesting article about error handling in a functional way in Scala and some ideas that make it possible to deal with failures in a very simple,...
Darwin is a lightweight repository written in Scala that allows to maintain different versions of the Avro schemas used in your applications. It is...
How a developer can remotely debug a running Spark Scala/Java application (running on YARN) using IntelliJ IDEA